LiFiDeA의 검색 이야기 

지난회까지 확률의 기본 개념 및 확률과 관련하여 범하기 쉬운 오류에 대해 알아보았습니다. 이번에는 확률 지식을 실전에 응용하는데 기본이 되는 확률분포를 알아보겠습니다. 확률의 개념을 이해하면 됬지 왜 여러 종류의 확률분포를 또 공부해야 되냐구요?

이렇게 생각해봅시다. 객체지향 설계에서 복잡한 요구사항을 디자인 패턴의 조합으로 해결하듯이, 확률분포는 복잡한 실제 현상을 단순한 확률모형의 조합으로 이해하기 위한 도구입니다. 현상을 확률적인 특성에 따라 몇 가지로 구분하고 각각에 대해 필요한 값(확률분포함수, 평균, 분산 등)을 미리 계산해 놓았으니 고맙기 이를데 없습니다.

복잡한 현상을 확률분포 몇가지의 조합으로 분석할 수 있다는 사실도 놀랍거니와, 임의의 확률분포에서 추출한 표본이 정규분포를 따른다는 신비로운 특성도 보입니다.

이항분포(Binomial Distribution)

가장 단순한 확률분포로, 앞면이 p의 확률로 나오는 동전을 N번 던졌을 때 나오는 앞면의 개수가 이루는 확률분포입니다. 앞면 혹은 뒷면으로 결과를 구분할때와는 달리 결과가 숫자이므로, 이를 좌표평면에 표시할 수 있습니다. 기본 조건인 동전의 성질(p)와 시행 횟수만 알면 평균은 Np, 분산은 Np(1-p)로 구해집니다.

포아송분포(Poisson Distribution)

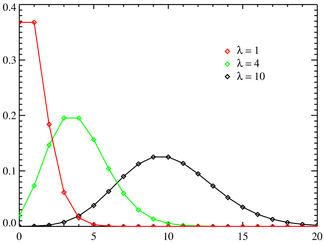시간당 5명의 손님이 오는 가게에서 일한다고 생각해 봅시다. 바로 이 순간에 손님이 도착할 확률은 0에 가까우나, 순간이 무한히 모여 이루어지는 기간(1시간)에 대해서는 일정한 확률(5명)이 정의됩니다. 이를 표현하는 확률분포가 포아송분포로서, 앞서 살펴본 이항분포에서 성공률이 극히 작은(p->0) 대신 시행횟수가 매우 큰(N->무한대) 경우라고 생각하면 편합니다.

실제 시/공간에서 벌어지는 일은 대부분 여기에 해당되기에, 포아송분포는 쓸모가 많습니다. 예를 들어 일정한 횟수와 분포로 발생하는 사건을 다루는 대기행렬 이론(Queueing Theory)의 기초가 되기도 합니다. 큐잉 이론은 다음 회에서 다시 다루도록 하겠습니다.

k : 사건의 실제 발생 횟수
λ : 단위 기간동안 예상 발생 횟수
 
위와 같은 포아송분포를 k를 x축으로 갖는 확률분포 그래프로 그리면 위와 같습니다. 그림에서처럼 λ가 4인 경우 4에서 가장 높은 확률을 보입니다. (기간 당 예상 발생 횟수가 4이니 당연합니다.)

지수분포(Exponential Distribution)

  사건의 발생 확률이 지수적(exponential)으로 감소하는 분포를 지수분포라고 합니다. 예컨데 단위 길이를 뚫을 확률(강성)이  λ인 금속판을 어떤 입자가 a보다 깊게 뚫는 사건을 생각해봅시다. 이를 두께가 1/n으로 무한히 얇은 금속판을 n*a번 뚫는 사건으로 볼 수 있으며, 이에 따른 확률분포는 아래와 같습니다.

이 성질은 지수분포가 다양한 현상을 모델링하는데 사용되는 이유가 되니, 잘 알아둡시다.

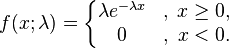
정규분포와 중심극한정리(Central Limit Theorem)

이공계 대학생이라면 누구나 배우는 것이 중심극한정리입니다. 요약하면 임의의 서로 독립적인 확률분포(모분포)에서 추출된 값들의 합(표본 평균)은 원래 모분포의 종류와 관계없이 정규분포를 이룬다는 겁니다. 다음 웹페이지에는 다양한 모분포에 대해 표본 평균이 정규분포가 됨을 애니메이션으로 보입니다. 이때 정규분포의 평균은 모분포의 평균과 동일하나, 분산은 모분포의 분산을 추출한 횟수(표본 크기)로 나눈 값입니다. (여러번 추출하여 평균한 값에 대한 분포이니 당연히 분산이 줄어들게 됩니다.)

중심극한정리를 모집단과 표본집단의 관계를 설명하는 것으로 이해할 수 있는데, 모집단을 모두 조사하기 힘든 경우 표본 조사를 수행하고 이를 통해 모집단의 평균 및 분산을 역으로 추정할 수 있는 것입니다.

중심극한정리를 이해하면 정규분포가 왜 그렇게 광범위하게 나타나며, 또한 활용되는지 알 수 있습니다. 많은 현상이 단일 확률분포를 따른다기보다 확률분포에서 추출된 여러 값의 합으로 묘사될 수 있는데, 이 합은 어김없이 정규분포를 따르기 때문입니다. 따라서 자연계의 현상(예:신호의 노이즈) 분석 및 표본추출에 근거한 사회현상 분석에는 대부분 정규분포가 사용됩니다.

참고자료

강의자료

통계 정보 홈페이지 (전북대 통계정보학과 / 친절한 설명이 인상적입니다.)
확률론과 확률분포
표본이론과 중심극한이론

확률분포
http://en.wikipedia.org/wiki/Probability_distribution
http://en.wikipedia.org/wiki/Binomial_distribution
http://en.wikipedia.org/wikiPoisson_distribution
http://en.wikipedia.org/wiki/Exponential_distribution


중심극한정리
http://en.wikipedia.org/wiki/Illustration_of_the_central_limit_theorem
http://en.wikipedia.org/wiki/Concrete_illustration_of_the_central_limit_theorem
중심극한정리 컴퓨터 시뮬레이션

(모든 그림은 위키피디아에서 차용하였습니다.)

교과서를 가지고 씨름하다 혹시나 해서 도서관에 가 보았는데, 역시 쓸만한 책이 많더군요. 교과서보다 훨씬 생생한 사례를 가지고 알기쉽게 설명한 책을 찾았습니다. 지난 시간에 소개한 '통계는 성공의 나침반'이라는 책을 추천합니다. 다음 구절이 인상적이어서 옮겨 보았습니다.

"인간의 두뇌는 확률문제를 푸는 데 별로 적합하지 않다." - 책 '확률의 함정'에서

위 말처럼 인간의 사고 및 판단의 대부분을 차지하는 휴리스틱(Heuristic)은 오류투성이여서, 정신이 온전한 상태에서도 수많은 실수를 범하게 됩니다. 오늘은 확률과 관련하여 자주 범하는 오류를 살펴보도록 합시다.

부분의 합은 전체가 아니다? - 심슨의 역설

직관과 어긋나는 사례로 자주 언급되는 것이 '심슨의 역설(Simpson's Paradox)'입니다. 이는 발견자인 에드워드 심슨 박사의 이름을 딴 것으로, 통계 조사에서 부분적인 결과와 이를 합친 전체의 결과가 어긋나는 결과나 종종 관찰된다는 점을 지적합니다. 다음 기사는 어떤 대학의 남학생 합격률이 더 높았는데, 단과대별로는 여학생의 합격률이 높다는 모순적인 현상을 다룬 것입니다. 원인은 남학생은 대부분 합격률이 높은 단과대에 지원했으며, 여학생은 그 반대이기 때문입니다. 전체 합격자 비율은 단대별 합격률의 단순 평균이 아니라 전체 합격자 수를 전체 지원자 수로 나눈 것이므로, 합격자 절대수가 많으면 합격률이 높아지는 겁니다.

또 어떤 블로그에는 이를 빌어 한의학과 서양 의학을 비교하는 사례가 있군요. 과학자가 아니더라도 직관을 맹신하는 것은 위험합니다.

암검사 결과를 믿을 수 없다? - 베이즈 룰

많은 기계학습 이론의 기초가 되는 베이즈 규칙(Bayes' Rule)도 직관의 함정을 피하도록 도와줍니다. 다음 웹페이지는 어떤 암 발병확률이 1%이고, 발병자 80%가 양성 반응을, 비 발병자 9.6%가 양성 반응을 보이는 암검사에서 양성판정을 받은 환자가 암을 가졌을 확률이 몇%인지 묻고 있습니다. 실제 의사들에게 질문을 했을때도 대부분이 80%로 대답했다고 합니다만, 위 페이지의 계산결과를 보면 실제 확률은 7.8%라고 합니다. 이처럼 베이즈 규칙은 결과적인 사건(암검사)이 주어졌을 때 원인이 되는 사건의 확률을 추론할 수 있는 수단을 제공한다는 데 의의가 있습니다.

베이즈 규칙에서는 아래 식처럼 사건의 원래 발생확률(A - prior)과 그 사건이 발생을 가정할때 현상이 나타날 조건부 확률(B|A likelihood - 해당 사건이 현상을 설명하는 정도)를 곱해서, 현상이 주어졌을때 예측하고자 하는 사건의 발생 확률(A|B posterior)을 계산합니다. 앞의 사례로 돌아가면, 암(사건)의 발병확률이 1%로 워낙 낮기 때문에, 양성판정(현상)으로 높아진 확률도 7.8%에 머무는 것입니다.


기계학습의 주제인 분류(classification)작업에서는 현상에 대한 학습자의 가설(hypothesis)이 사용되기에,  주어진 현상(B)을 가장 잘 설명하는 가설(A)을 찾는데 베이즈 규칙을 사용합니다. 베이즈 룰을 사용한 스팸 필터를 생각해보면 메일에 포함된 단어(B)를 종합하여 스펨인지 아닌지(A)를 판단해 내는 것입니다.

마치며

베이즈 규칙은 기계학습 알고리즘 대부분의 이론적 기초를 제공하는 중요한 이론이지만 그 함의를 완전히 이해하는 것은 쉬운 일이 아닙니다. 제 이해가 부족한 모양인지, 이 부분을 보통 대학생이 이해할 수 있을 정도로 설명했다는 확신이 서지 않네요. 공부를 더 쌓으며 보충하도록 하겠습니다. 다음에는 확률 분포를 다룰까 합니다.

참고자료

심프슨의 역설

심프슨의 역설 관련 기사

http://en.wikipedia.org/wiki/Simpson's_paradox

베이즈룰

http://en.wikipedia.org/wiki/Bayes_rule

An Intuitive Explanation of Bayesian Reasoning

학문 연구는 결국 현실 세계의 문제를 푸는데 그 목적이 있을진데, 대부분 사람에게는 멀게만 느껴집니다. 지식 자체의 복잡성보다도 이를 전달하는 방식에 대한 고민이 부족하지 않았나 합니다. 교과서는 딱딱한데다 현재 추세에는 한참 뒤쳐지며, 신선한 연구결과를 담은 논문은 그 분야 전문가 몇몇을 제외하고는 읽어볼 엄두조차 못내는 것이 우리의 현실입니다.

운영 계획에서 밝힌 대로 이론적 지식을 대중의 눈높이에 맞추어 소개하려고 합니다. 학문적 엄밀함보다는 활용가능성에 초점을 맞추어, 상식보다 한걸음 나아가는 앎의 전달을 목표로 합니다. 쉽게 설명하기 위해서는 제대로 알아야 하므로, 저의 공부에도 도움이 되지 않을까 합니다.

첫번째로 확률론을 다루겠습니다. 고등학교 졸업한지 몇년이상 되신 분들은 거의 기억나지 않으시겠으나, 확률론은 생각보다 쓸모가 많습니다. 세상 대부분이 비결정적인 확률적 현상이기에, 확률에 대한 지식은 좀더 정확한 예측 및 판단을 가능케하며, 자칫 범하기 쉬운 오류도 막아줍니다. 좀더 섬세하고 정확한 직관을 주는 것입니다.

또한 확률론은 많은 학문의 기초가 됩니다. 기계학습(Machine Learning)은 확률론을 계산모델로 표현한 것이며, 자연어처리(Natural Language Processing) 및 정보검색(Information Retrieval)분야에서도 최근에는 확률론을 적용하여 정확도를 높이고, 예외 상황에 강한 이론 및 시스템을 만들고 있습니다.

확률을 아십니까

자주 쓰는 용어의 엄밀한 정의를 내리기 힘든 경우가 많은데, '확률'도 만만한 개념은 아닙니다. 확률은 결국 정보의 정확성에 대한 개념일진데 최근에 읽은 책에서는 이를 다음과 같이 구분합니다.

1. 확실 : 결과가 결정된 경우
2. 리스크 : 결과의 종류 및 각각의 확률을 아는 경우
3. 불확실 : 결과의 종류 혹은 각각의 확률이 불확실한 경우
   
4. 무지 : 결과에 대해 전혀 모르는 경우

실제로 사용되는 확률은 2, 3번의 정의를 포괄합니다. 또한 2번에서 언급된 '앎'의 객관성에 따라 객관적 / 주관적 확률로 구분되기도 합니다. 이중 '객관적 확률'은 주사위의 각 면이 나올 확률처럼 실험에 의해 검증가능한 것이며, '주관적 확률'은 내가 이번학기에 여자친구를 사귈 확률처럼 현상에 대한 개인의 확신의 정도를 나타냅니다. 이는 당연히 같은 현상에 대해 사람마다 다를 수 있습니다.

여기서 '직접 실험해볼 수 없는 확률은 모두 주관적이란 말이냐'는 의심을 가지실 수 있습니다. 만약 그렇다면 확률 공부하는 사람은 앉아서 숫자 세는 것 이외에는 할 일이 없겠지만 그렇지는 않습니다. 실제로는 알려진 사건에 법칙을 적용하여 알려지지 않은 사건의 확률을 추론해낼 수 있으며, 이렇게 구한 확률을 '논리적 확률'이라고 합니다. 이는 실제로 객관화될 수 있는 값이나, 검증되지 않았다는 측면에서는 객관적 확률은 아닌 듯 합니다.

확률론의 세계관

다른 학문이 그렇듯이 확률론에서도 세계를 바라보는 고유한 관점을 갖습니다.  확률론의 세계는 발생가능한 모든 사건을 포함하는 '표본공간'(Sample Space)입니다. 표본공간이 사건 전체의 집합이라면 '사건'은 표본공간의 부분집합이며, 각각 고유의 발생 가능성 - '확률' - 을 가집니다. 확률론에서 가장 많이 사용되는 동전 던지기를 생각해봅시다. 여기서 표본공간은 앞면과 뒷면이며, 보통 동전이라면 앞면 혹은 뒷면이 나올 확률이 각각 1/2입니다. 표본공간 전체의 확률은 1이겠죠.

너무 시시하다구요? 하지만 옛부터 튼튼한 개념이 학습의 지름길이라고 했습니다. 확률론의 다른 개념은 모두 여기에서 파생되며, 좀더 복잡한 현상을 확률론으로 설명하다보면 표본공간과 사건의 개념이 흔들리기 일쑤입니다. 동전을 N번 던져 앞면이 나오는 횟수를 조사할 경우 표본공간은 무엇일까요? 서로 구별가능한 동전을 N개 같이 던질때는 어떻게 될까요?

사건간의 관계

표본공간과 사건을 정의한 후에 생각해볼 것이 사건 간의 관계입니다. 예방접종을 맞으면 질병에 걸릴 확률이 낮아지는 것처럼 사건 간에는 다양한 의존관계가 존재합니다. 여기서 조건부 확률의 개념이 등장합니다. 특정 사건 B(조건)의 발생 여부가 원래 사건 A의 발생 확률에 영향을 끼치는 것입니다. B의 발생을 아는 상태에서의 확률은 원래 알던 A의 확률 P(A)와 구분지어 P(A|B)로 표시합니다.

이와 관련하여 생각해 볼수있는 것이 사건 간의 독립성입니다. 독립적으로 발생하는 두 사건간의 관계는 어떤 특성을 지닐까요? 직관적으로는 한 사건의 발생 확률이 다른 사건의 확률에 영향을 끼치지 않아야 합니다. 조건부 확률을 이용해 표시하면 P(A) = P(A|B)가 되겠군요.

주의할 점은 셋 이상의 사건이 있을때 두 사건씩 쌍으로 독립인 것과, 세 사건이 서로 득립인 것은 구분해 주어야 한다는 것입니다. 즉, A,B,C에 대해 생각해보면 A와 B각각은 C와 독립이지만, A와 B가 동시에 발생하는 사건은 C에 영향을 줄 수 있다는 겁니다. 슬슬 직관이 어긋나기 시작하시나요?

복잡한 확률 문제 풀기

실 세계의 사건은 대부분 단순한 규칙 적용으로 풀리지 않습니다. 어디서부터 손대야 할지도 막막한 경우가 대부분입니다. 이럴때 전가의 보도처럼 사용되는 방식이 Divide & Conquer입니다. 확률론에도 이처럼 복잡한 현상을 나누어 해결하도록 도와주는 도구가 있는데, 이것이 전확률법칙(Law of total probability)입니다.


전확률법칙은 위 식처럼 복잡한 사건 A의 확률을 바로 구하기보다 사건 B1~Bn에 대한 조건부 확률의 가중평균으로 구하는 겁니다. 여기서, 사건 B1~Bn은 표본공간 전체에 대한 분할이어야 합니다. 전교에서 어떤 혈액형을 가진 학생의 비율을 구할때, 반별로 구한 비율을 반별 학생수로 가중평균하여 구하는 방식입니다. 물론 실제 사건에 대한 적절한 분할을 찾는 문제는 이처럼 단순하지는 않겠죠.

다음에는...

저의 연구분야 - 머신러닝 / 정보검색 - 가 대부분 확률론에 기반하기에, 이 글은 앞으로 다룰 많은 주제의 기반이 될 듯 합니다. 다음에는 확률 현상과 관련된 흔한 오류를 다룰까 합니다.

참고자료

위 자료는 '확률의 개념 및 응용 - 전종우/손건태'에 기초하며, 아래 자료는 추가로 읽어보시기 바랍니다.

Stanford Univ. Probabillity Theory Textbook (PDF)
Java Applets on Probability Theory

통계학 관련 블로그
류근관 교수님의 통계학 홈페이지

http://en.wikipedia.org/wiki/Probability_theory

http://en.wikipedia.org/wiki/Probability_interpretations

http://en.wikipedia.org/wiki/List_of_probability_topics
http://en.wikipedia.org/wiki/Law_of_total_probability