불확실성을 평가한다 -- 정보이론(Information Theory)
정보 이론은 기계학습이나 자연어처리, 정보검색을 연구하는 사람에게 기본 소양처럼 여겨지는 분야입니다. 하지만 처음에는 정보를 계량적으로 측정한다는 발상 자체부터 와닿지 않았습니다. 지난 학기에 공부한 내용을 바탕으로 정보이론에 대한 직관적 이해를 돕는 글을 써 보려 합니다.
확률론이 불확실성에 대한 모델링과 이에 기반한 추론을 목표로 한다면, 정보이론은 불확실성을 평가하려 합니다. 정보이론의 ’정보’는 불확실성인 다름아닌 것입니다. 따라서 정보이론의 가장 기본적인 단위인 엔트로피(Entropy)의 계산에도 확률변수가 사용됩니다.
대부분의 대상이 확률변수로 모델링되는 위 분야에서 정보이론이 항상 사용되는 것은 놀라운 일이 아닙니다. 예를 들어 정보검색 분야에서는 문서와 질의어(query)를 확률변수로 모델링하고 이 모델간의 거리를 바탕으로 문서의 랭킹을 계산하는데, 이때 사용되는 척도(KL-Divergence)가 정보이론에서 제공됩니다.
좀더 구체적으로 알아봅시다. 확률변수 X의 불확실성을 나타내는 엔트로피는 다음 수식처럼 각 확률값에 로그를 취한 것의 기대값(즉, 확률값에 대한 가중 평균)으로 계산됩니다.
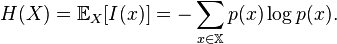
간단한 루비 프로그램으로 이를 알아봅시다. 아래 예에서 보듯 두가지 사건이 가능한 확률변수의 경우 각 사건의 발생 확률이 균일할수록 엔트로피는 커집니다. 이는 엔트로피를 불확실성으로 이해할 때, 사건간의 확률이 비슷할수록 예측하기 어렵다는 점과 통합니다.
>> [1,1].to_prob.h
=> 1.0
>> [1,5].to_prob.h
=> 0.650022421648354
>> [1,10].to_prob.h
=> 0.439496986921513
>> [1,100].to_prob.h
=> 0.0801360473312753
>>
또한, 표본공간을 잘게 쪼갤수록 엔트로피(불확실성)는 더 커집니다.
>> [1,1].to_prob.h
=> 1.0
>> [1,1,1,1].to_prob.h
=> 2.0
>> [1,1,1,1,1,1,1,1].to_prob.h
=> 3.0
엔트로피에 대한 연산
확률변수 여러개가 모여 연합확률분포(Joint Probability Distribution)를 형성하고 확률변수간에 조건부확률(Conditional Probability)를 정의할 수 있는 것처럼 연합 엔트로피나 조건부 엔트로피도 정의될 수 있으며, 이러한 값들에 대한 연산 법칙은 확률변수의 경우와 마찬가지로 적용됩니다.

상호 정보(Mutual Information)
개별 사건의 불확실성을 평가하다 보면 자연히 두 사건간의 관계에 관심이 가게 됩니다. 두 사건간의 의존성을 불확실성 관점에서 평가하는 것이 상호정보입니다. 즉, 사건 와
가 있을 때,
를 아는 것이
의 불확실성을 얼마나 낮추어주는지를 평가하는 겁니다.

이는 를 기준으로 다음처럼 기술할 수도 있습니다.

Cross Entropy & KL-Divergence
앞서 설명한 것처럼 현상을 확률번수로 모델링하다보면 필수적인 과정이 우리가 만든 모델을 실제 현상에 비추어 평가하는 것입니다. 즉, 우리가 만든 모델이 얼마나 대상에 부합하는지를 평가할 수 있어야 이를 개선시킬 수 있는데, 이때 척도로 사용되는 것이 KL-Divergence입니다. 앞서 설명한 정보검색 예제에서는 각 문서를 질의어로 상징되는 유저의 정보욕구(Information Needs) 대한 모델로 보고, 이에 부합하는 순서대로 랭킹을 계산하는 겁니다.

구체적으로 KL-Divergence는 우리가 모델링하려는 사건에 대한 확률변수 를 불완전한 모델
를 사용하여 표현하는 데 필요한 비트 수를 뜻하는 Cross Entropy에서 원래 사건의
의 엔트로피를 빼서 구합니다. 즉,
를 통한 모델링 작업이 얼마나 실제 사건
의 불확실성을 증가시켰는지를 나타내는 것입니다.
앞서 설명한 상호정보 역시 KL-Divergence를 사용하여 표현될 수 있습니다. 아래 식을 보면 사건 와
의 연합확률분포
를 각 사건의 확률분포
와
의 곱으로 나타낼 때 더 필요한 비트의 수가 두 사건간의 상호정보라는 것을 알 수 있습니다.

다시 루비 예제를 봅시다. 두 사건간의 Cross Entropy는 아래처럼 두 사건의 확률분포가 비슷할수록 작다는 것을 알 수 있습니다.
>> [1,2,3].to_prob.h
=> 1.45914791702724
>> [1,2,3].to_prob.ch([1,2,3].to_prob)
=> 1.45914791702724
>> [1,2,3].to_prob.ch([3,2,1].to_prob)
=> 1.98746875060096
>> [1,2,3].to_prob.ch([10,2,1].to_prob)
=> 2.81345170232653
Reference
소스 코드
위 예제를 실행시키기 위해서는 다음 모듈을 Array에 Include하면 됩니다.
module Entropy
include Math
## Get probability distribution
def to_p()
collect{|e| e.to_f / sum}
end
## Entropy
def h
-inject(0){|sum,e| sum + e * log2(e) }
end
## Cross Entropy
def ch(a)
sum = 0 ; each_both(a){|p , q| sum += p * log2(q) } ; -sum
end
## KL-Divergence
def kld(a)
ch(a) - h()
end
end
'검색공부하기' 카테고리의 다른 글
| 새로운 알고리즘의 성능이 훌륭한가? - 유의성 테스트 (0) | 2008.11.03 |
|---|---|
| 정보 검색(Information Retrieval)을 연구한다고? (1) | 2007.10.03 |
| 다시 배우는 선형대수(1) - 우리곁의 벡터와 행렬 (11) | 2007.05.20 |

